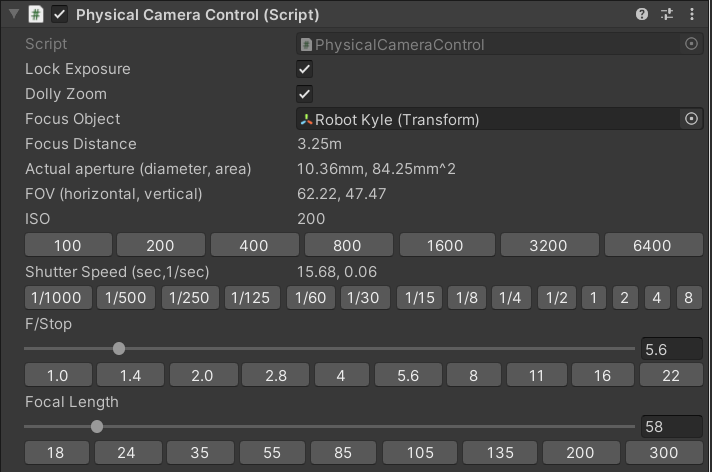
Unity HDRP has a physical section on it’s camera component. It mimics real-life camera settings like sensor, size, ISO, focal length and aperture. These settings are used by the camera itself, but also by other systems that affect rendering, like the Exposure and Depth of Field volume overrides.

This allows someone who is familiar with cameras to operate within Unity. But it also helps the user setup physically realistic camera settings, all in one place.

The settings in physical camera are simply raw values, so can be difficult to get right. I made a component that sits along side the camera component to help with this.

Current features:

• Standard camera presets for ISO, F/Stop and focal lengths.
• Exposure locking by automatically adjusting shutter speed or aperture settings. Makes it easy to set up depth of field.
• Dolly zoom to make it easy to frame a shot while adjusting the focal length.

Find the project on Github.

Here’s a short tutorial video on the the physical camera settings and using this component to frame and expose a shot.

Update (20/02/20)

The NativeContainerIsAtomicWriteOnly attribute is required for use in IJobParallelFor, but it also means the container is marked as write only! If you use it in a IJobParallelFor and attempt to read a value which is checked with AtomicSafetyHandle.CheckReadAndThrow(m_Safety);, then you’ll get the error When accessing: InvalidOperationException: The native container has been declared as [WriteOnly] in the job, but you are reading from it.

So two separate containers are required.

• A write only container that uses the NativeContainerIsAtomicWriteOnly attribute.
• A read and write container without this attribute for use in IJobs. You can optional mark this as read only with the [ReadOnly] attribute.

Note you can use a container that is not marked as atomic write only in an IJobParallelFor if the field in the job has a NativeDisableParallelForRestriction attribute.

This impossible without copying and pasting code. structs don’t have inheritance, you can’t use an interface in a job. You can’t use a third shared class for implementation with two light wrappers around it. The DisposeSentinel is not blittable and can’t be used in this class. So none of the safety checks can go in the third class. Which in this case is the majority of the code.

Passing Data to Jobs

Jobs in Unity must be structs and must only contain blittable types. This allows jobs to be copyable and for the job system to enforce thread safety. If I have a job with an int field, the value of the int is copied and I have no way to get the result of my fancy calculation I performed in the job.

You have a NativeArray of floats and and want to add a number to each element. You make an addition job. Easy!

[BurstCompile(FloatPrecision.Standard, FloatMode.Fast, CompileSynchronously = true)]
public struct AdditionJob : IJobParallelFor
{
    [ReadOnly] public float NumberToAdd;
    public NativeArray<float> Values;

    public void Execute(int index)
    {
        Values[index] += NumberToAdd;
    }
}

(Part of a series where I think out loud about an out-of-core point cloud renderer I’m working on.)

A sparse array uss the classic programming trick of adding another layer of indirection. Not by using a pointer, but by adding an abstraction over a traditional array.

I’m in the process of building an Octree for use in a Point Cloud Renderer. The Octree will store nodes layer by layer. This means that some layers will have mostly empty space. Rather then storing the nodes directly, this sparse array has two arrays, one to store the data and the other to store the indices of the data. The data is always sorted, so a binary search can be used to find data or insertion points for adding data.

(Part of a series where I think out loud about an out-of-core point cloud renderer I’m working on.)

Morton encoding is a perfect set up for Burst, lots of data in a row to crunch!

So what happens when I turn it on? In order to use Burst, we need to have our code in a job.

Morton Order

For the out-of-core point cloud renderer I’m working on I need a way to convert a node coordinate into an array index. The idea is all nodes in a layer and children of a node should be in contiguous memory for easy access and cache friendly processing.

In my first implementation I used Hilbert curves. They guarantee each array index will be a next-door neighbour node, but they are reasonably complex to calculate. Morton order guarantees the 8 children of a node will be contiguous, but there may be discontinuities between those blocks.

Infinite Points - Introduction

It’s becoming more and more common to use photogrammetry and lidar scanning to capture buildings, engineering projects, sites of cultural significance, archaeological digs, etc. Most of these points clouds are in the billions of points; slow to render and unable to fit into memory.

There are workflows for converting point cloud data into meshes, but the process is usually laborious and data is lost in the process. For digs or remote inspections keeping all the point cloud data is very important.

I’d like to build an out-of-core point cloud renderer for Unity that solves these issues but keeping parts of the point cloud data on disk and reading in the most important data for the users viewpoint.

I’ve been wanting to learn more about Angular.JS so made a quick web page to view the location all of Melbourne’s public art on a Google Map.

There is an amazing amount of open data on the web. The Australian government has been releasing its data through data.gov.au. The dataset of all Melbourne’s public art seemed like a great place to start.

I used the AngularJS Google Maps directives. It provdes a promise that gets called when Google Maps is loaded and ready to go. Then I fire off a http request to data.gov.au, with yet another promise that extracts the marker data and sets it the data bound markers array.

Fluid Simulation to Generate a Flow Map

Here is a proof of concept of using a 2D fluid simluation to generate a Flow Map. This follows on from my Fluid/Flow Map ShaderToy experiment to do the same thing, except here I have a much better fluid simulation.

Press the ‘f’ key to swap between the fluid simulation and the flow map. When the flow map is being displayed the fluid simulation stops.

This could be used in a game to deal with dynamic obstacles in water or smoke, without having to run a full fluid simulation all the time. The fluid simulation could be amortised over many frames, leading to a cheap fluid effect.

The implmentation is in ThreeJs/WebGL, check the source code of this page for details.

Following on from my previous Flow Map post, I wanted to see what flow maps would look like with maps generated in real time using a fluid sim.

Flow maps are a simple way to get some movement into your shader. Valve and The Wild External have documented the process pretty throughly.

I thought I’d try a GLSL/Three.js implmentation.

The three.js introduction introduction for setting up a scene suggests you dynamically append a canvas to the document. Totally screwing up your nicely formatted blog.